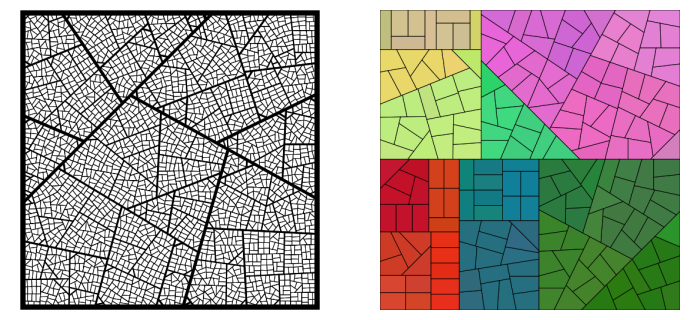
Fat Polygonal Partitions with Applications to Visualization and Embeddings
Abstract: Let $\mathcal T$ be a rooted and weighted tree, where the weight of any node is equal to the sum of the weights of its children. The popular Treemap algorithm visualizes such a tree as a hierarchical partition of a square into rectangles, where the area of the rectangle corresponding to any node in $\mathcal T$ is equal to the weight of that node. The aspect ratio of the rectangles in such a rectangular partition necessarily depends on the weights and can become arbitrarily high.
We introduce a new hierarchical partition scheme, called a polygonal partition, which uses convex polygons rather than just rectangles. We present two methods for constructing polygonal partitions, both having guarantees on the worst-case aspect ratio of the constructed polygons; in particular, both methods guarantee a bound on the aspect ratio that is independent of the weights of the nodes.
We also consider rectangular partitions with slack, where the areas of the rectangles may differ slightly from the weights of the corresponding nodes. We show that this makes it possible to obtain partitions with constant aspect ratio. This result generalizes to hyper-rectangular partitions in $\mathbb{R}^d$. We use these partitions with slack for embedding ultrametrics into $d$-dimensional Euclidean space: we give a $ \operatorname{polylog}(\Delta)$-approximation algorithm for embedding $n$-point ultrametrics into $\mathbb{R}^d$ with minimum distortion, where $\Delta$ denotes the spread of the metric, i.e., the ratio between the largest and the smallest distance between two points. The previously best-known approximation ratio for this problem was polynomial in $n$. This is the first algorithm for embedding a non-trivial family of weighted-graph metrics into a space of constant dimension that achieves polylogarithmic approximation ratio.